Heinz Siebert
Lücken zwischen Primzahlen 25.04.2002
Programm | Ergebnisse | Bewertung des Ergebnisses L | Bewertung des Ergebnisses mL | Diagramm | Download | Kontakt | zurück
1. Programm
Betrachtet man die Differenzen zwischen benachbarten Primzahlen (hier als Lücken bezeichnet),
so ergeben sich einige Besonderheiten, die mit Hilfe eines C++-Programms festgestellt wurden.
So wächst mit steigender Größe der Primzahl die maximale Lücke, jedoch
ohne einer sichtbaren Regel zu folgen; dagegen wächst die mittlere Größe aller
Lücken so gleichmäßig mit dem Logarithmus der Primzahl, das man sie näherungsweise
berechnen kann und damit auch die Zahl der Primzahlen.
Das Programm ermittelt die größten Lücken L zwischen den Primzahlen, wobei
angegeben ist, wo diese erstmalig auftritt (bei Prim). Das wiederholte Auftreten einer gleich
großen Lücke wird nicht berücksichtigt.
2. Ergebnisse
Anhand der Ergebnisse des beigefügten Programms soll das näher erklärt werden:
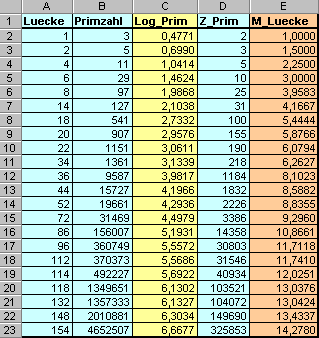
Beispielhaft soll die markierte 3. Zeile für Erklärungen verwendet werden.
L ist die Differenz zwischen der Primzahl Pn (hier 11) und der nächst kleineren Primzahl
P(n-1) hier 7; d.h. L=11-7 = 4.
Zahl Prim ist die Anzahl der Primzahlen bis Pn, hier 2,3,5,7,11, also 5
mL ist die mittlere Lücke = Summe aller Lücken durch Zahl aller Lücken bis Pn.
Die Summe aller Lücken ergibt sich aus Pn - 2; im Zahlenbeispiel 3-2+5-3+7-5+11-7 = 11-2
Die Zahl aller Lücken ergibt sich aus Zahl Prim - 1, im Beispiel 4
damit wird mL = Pn-2/Zahl_Prim -1; im Beispiel 9/4 = 2.25
3. Bewertung des Ergebnisses L
Betrachtet man die Lücken am Ende der Tabelle, so könnte man vermuten, dass eine
neue größere Lücke etwa bei einer Verdoppelung der untersuchten Zahlen, also
etwa bei Prim 8 Millionen auftreten müsste, was aber nicht der Fall ist. Eine größere
Lücke als 154 wurde auch nach 20 Stunden Rechenzeit nicht gefunden, d.h. bis zur Primzahl
13374617. Damit stellt sich die Frage nach einer Fortsetzung dieser Zahlenwerte; wer findet
oder kennt größere Primzahl-Lücken?
4. Bewertung des Ergebnisses mL
Im Gegensatz zur größten Lücke wächst die mittlere Lücke kontinuierlich
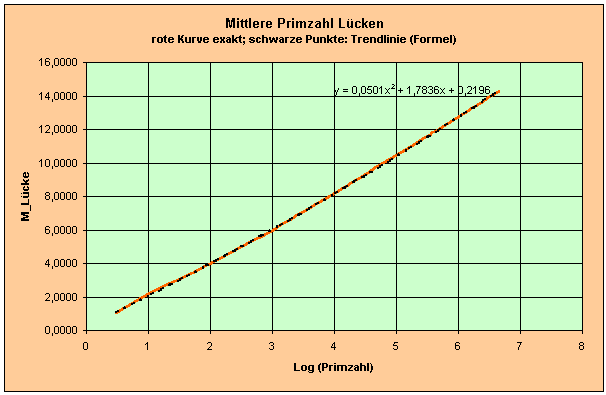
mit dem Logarithmus von Pn an, wie eine EXCEL Grafik zeigt, in der mL = f(log(Pn)) dargestellt
ist. Anhand einer Trendlinie berechnet EXCEL eine Näherungsformel y=0,0501*x*x+1,7836*x+0,2196
mit y=mL und x = log(Pn). Damit lässt sich aber nicht nur die mittlere Lücke berechnen,
sondern auch (näherungsweise) die Zahl der Primzahlen in einem beliebigen Intervall. Gemäß
der oben angegebenen Gleichung ist Zahl_Prim=(Pn-2/mL)+1 oder für große Zahlen Zahl_Prim=Pn/mL
5. Diagramm
Das Diagramm, dessen Kurvenverlauf für die sonst recht unberechenbaren Primzahlen erstaunlich
zahm verläuft.
x = Log_Prim, y = M_Lücke. Die Tabelle wird auch vom C++-Programm als Text-Datei bereitgestellt,
die sich dann in EXCEL laden läßt. Die Log-Spalte berechnet EXCEL.
6. Download
7. Kontakt
Bei Fragen, Anregungen, Vorschlägen, Kritiken und Bug-Reports schicken Sie bitte an Heinz Siebert eine E-Mail (Heinz.Siebert@surfeu.de)