Kodjo Kudiabor †
kanonischer Primfaktoren – Generator 09.02.2003
Erklärung | Kontakt | zurück
Die lange gesuchte mathematische Beziehung zwischen der Dezimalzahl (P ) und ihren Bausteinen,
den Primfaktoren, (p ) lautet: P = p m(2h +1)
Zu dem Ergebnis gelangt man mit dem Verfahren des kanonischen Primfaktoren –
Generators. Zerlegt man laufende Dezimalzahlen beliebigen Intervalls (z.B.:1234501 bis 1234600)
in die entsprechenden kanonischen (also aufsteigenden) Primfaktoren (29 x 42569 bis 2 x 2 x2
x 5 x 5 x 6173), so lässt sich eine Trendbildung erkennen (s. Seite 2/2). Verfolgt man
dies, entsteht aus der Analyse die Formulierung der obigen P / p -Gesetzmäßigkeit.
Die Bedeutung der Parameter in einem Beispiel:
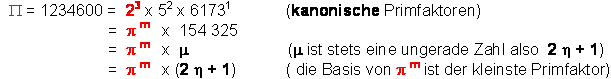
Die P / p -Gleichung beschreibt ein Orbital-Feld: Der kleinste Primfaktor p m gibt den Orbitalnamen
an. Die Orbitalzahl h bestimmt den Ort des Zahlen-Elements P auf dem Orbital. Dezimalzahlen,
die den gleichen p m – Faktor enthalten, liegen auf dem gleichen Orbital nach folgendem
Struktur-Beispiel

Der Abstand zwischen den Orbital-Elementen ist durch d =2 x p m definiert - ein Hinweis auf
die Antwort auf die Frage: Warum nimmt die Population der Primzahlen mir ihrer Größe
ab ?
Eine graphische Darstellung zeigt: das P / p - Orbital-Feld ist in einem Dreieck (Periodic
Triangle) organisiert. Die Gesamtheit dr natürlichen Zahlen liegt auf der senkrechten
Achse. Davon sind alle zusammengesetzten Dezimalzahlen (bestehend aus mindestens2 Primzahlen)
auf Orbitalen innerhalb des Dreiecks verteilt. Alle Primzahlen befinden sich auf der Hypotenuse
.und zwar in der bekannten scheinbar unregelmäßigen Folge: p1 = {2,3,5,7,11,13...}.
Die scheinbare Unregelmäßigkeit ist auf die Orbital-Organisation des natürlichen
Zahlensystems zurückzuführen ähnlich wie die scheinbare unregelmäßige
Zahlen-Folge: nS1={1,3,11,19,37,55,87}, die auf die Gruppe 1Â der Atome H,L1,Na,K,Rb,Cs,Fr
im Periodensystem zurückzuführen ist.

Bei Fragen, Anregungen, Vorschlägen, Kritiken und schicken Sie bitte mir eine E-Mail (webmaster@primzahlen.de)